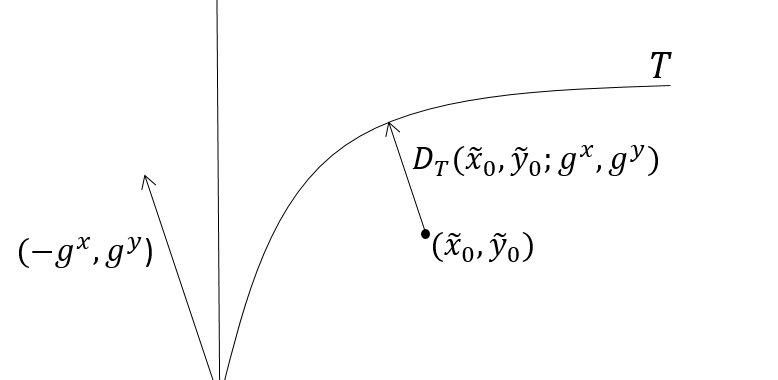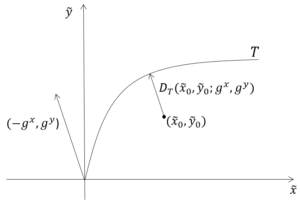
A distance function allows multiple product production using multiple resources to be modeled. A stochastic directional distance function (SDDF) allows for noise in potentially all input and output variables; however when estimated, the direction selected will affect the functional estimates because deviations from the estimated function are minimized in the specified direction. This paper addresses the question, how should the direction be selected to improve the estimates of the underlying production behavior. We are motivated by the estimation of a cost function for hospital production in the U.S., but our insights apply for production and distance functions as well. In contrast to the parameters of the parametric stochastic distance function which are point identified, we show that the parameters of the parametric SDDF are set identified when alternative directions are considered. We present simulation results that show if errors are uncorrelated across variables, then the benefit in terms of improved functional estimates from the use of a directional distance function are significant. Further, we show that these benefits grow as the correlation in error terms across variables grow. This correlation is a type of endogeneity that is common in production settings.
We show that the set of identified parameters for either the parametric or the nonparametric shape constrained estimator can be narrowed via data-driven approaches to restrict the directions considered.
We apply the SDDF estimation procedure to a data set of hospitals containing a sample of approximately 600 hospitals each year from 2005 to 2010. We propose to select a direction that is approximately orthogonal to the estimated function in the central region of the data and find this direction provides significantly better estimates of the cost function relative to other estimators.
Category Archives: Ongoing work
Shape Constrained Nonparametric IV Estimators for Production Function Estimation

We propose a shape constrained nonparametric IV estimator which imposes a set of shape constraints on a nonparametric IV approach. We apply the Landweber–Fridman regularization to the Shape Constrained Kernel–weighted Least Squares (SCKLS) estimator developed by Yagi et al. (2018). Furthermore, we also consider more complicated shape constraints proposed by microeconomic theory by applying iterative S–shape algorithm proposed by Yagi et al. (2018). We aim to improve the finite sample performance and the economic interpretability of estimated results by imposing correctly specified shape constraints while avoiding the bias from endogeneity issues.
Iterative S-shape production function estimation
A production function satisfying the Regular Ultra Passum (RUP) law is characterized by increasing returns to scale followed by decreasing returns to scale along any expansion path, which is referred to as S-shape function. Although there are existing nonparametric estimators imposing the RUP law, they impose additional strong assumptions such as: deterministic model, homotheticity or constant elasticity of scale. This paper proposes an iterative algorithm to estimate adaptively a function that satisfies the RUP law while relaxing these other assumptions.
Sweet or Sour? The Potential for U.S.-Cuban Trade in Sugar

This project seeks to analyze the potential for U.S.-Cuban sugar trade with a particular focus on Cuban sugar production. Cuba has historically been an important global sugar producer and U.S. sugar producers are sensitive to foreign competition. Furthermore, the potential for Cuban liberalization and subsequent possible inflow of foreign investment makes analysis of this industry important. The project’s implications are significant for U.S. sugar producers, U.S. national agricultural policy, and for agricultural development in developing countries generally.
Evaluating Production Function Estimators on Manufacturing Survey Data
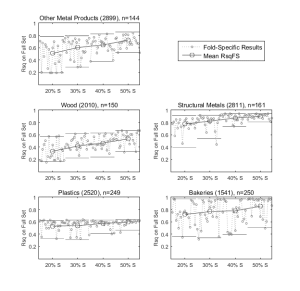
Organizations like census bureaus rely on non-exhaustive surveys to estimate industry population-level production functions. In this paper we propose selecting an estimator based on a weighting of its in-sample and predictive performance on actual application datasets. We compare Cobb-Douglas functional assumptions to existing nonparametric shape constrained estimators and a newly proposed estimated presented in this paper. For actual data, specifically the 2010 Chilean Annual National Industrial Survey, a Cobb-Douglas specification describes at least 90% as much variance as the best alternative estimators in practically all cases considered.
How inefficient are U.S. hospitals? What changes can lead to improvement?
We use U.S. hospital data from 2004 to 2011 to estimate a cost function using a Bayesisan semi-nonparametric method that allows for a heteroskedastic inefficiency. Moreover, we evaluate what is the impact of variables, such as region and hospital size, on cost estimating both the size and robustness of the variables in terms of reducing cost for hospitals.
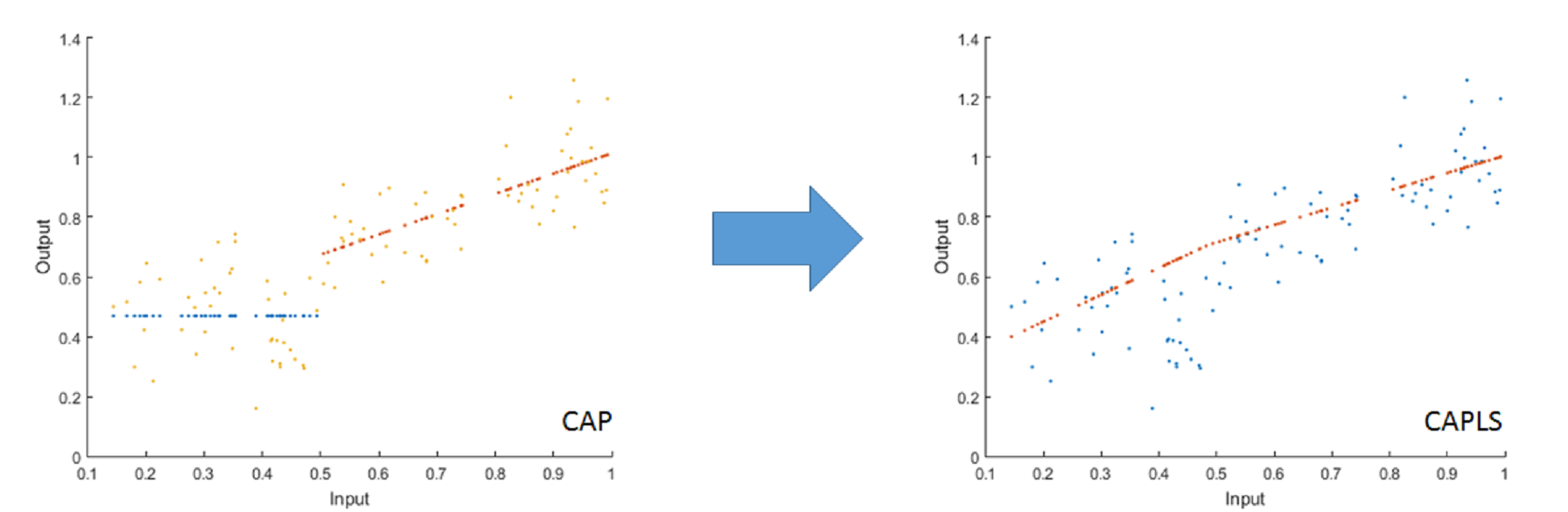
Adaptively Partitioned Convex Nonparametric Least Squares
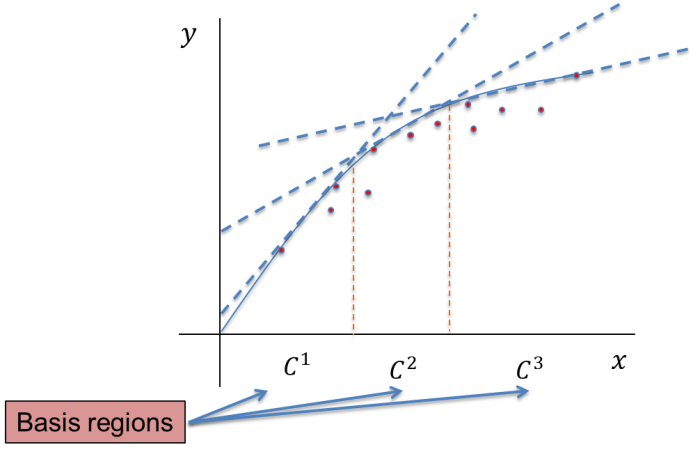
This research overcomes both the decreased accuracy of Convex Adaptive Partitioning on real production survey datasets and the cross-validation performance challenges of CNLS to create a robust and scalable adaptive partitioning-based convex regression method.
We discover that real production datasets often contain local monotonicity violations, which affect CAP’s ability to propose feasible basis region splits. Moreover, we note that CNLS’s error minimization strategy within the observed dataset results in poor estimations on unobserved firms due to over-fitting. We create a hybrid of both methods that preserves their most favorable properties at a small computational time expense. The paper summarizing this research is available on Arxiv.
Shape Constrained Kernel-weighted Least Squares (SCKLS)
SCKLS (shape constrained kernel-weighted least squares) estimator integrates kernel-weighting to convex nonparametric least squares.
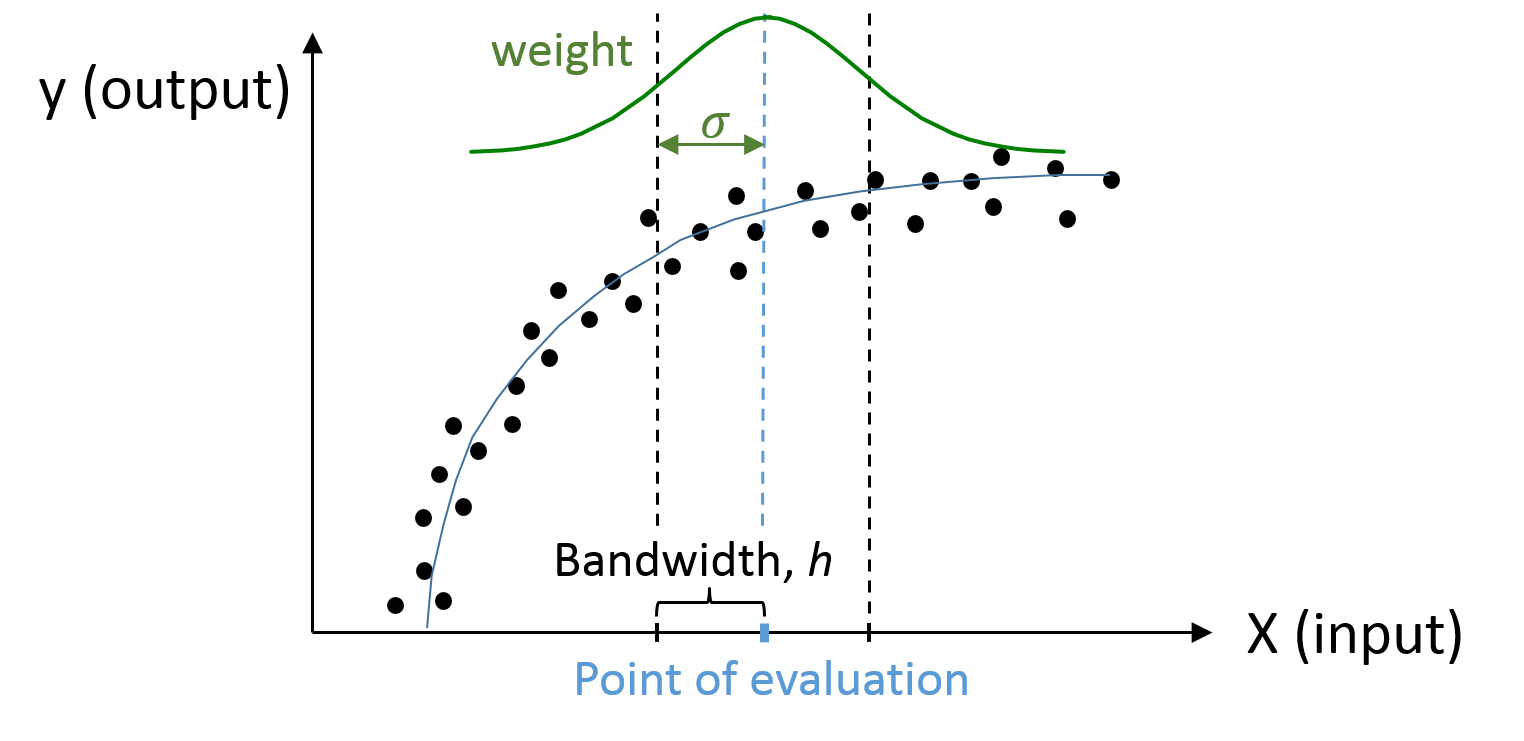
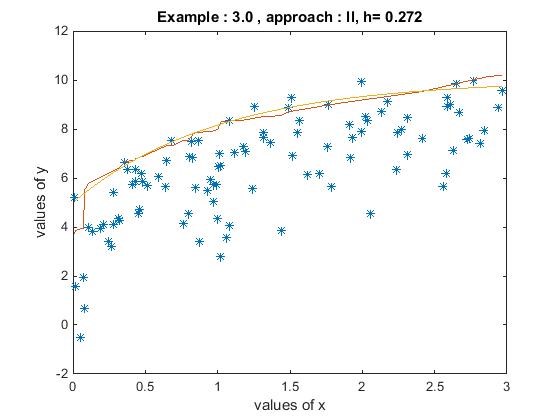
Kernel regression is one of the powerful nonparametric estimation methods. By imposing more weight to some closer points, kernel regression helps to avoid over-fitting although it requires the tuning parameter, bandwidth. By imposing some shape constraints such as monotonicity and concavity, we propose SCKLS estimator and apply it to estimate production function with simulated and real data. We also investigate the relationship with Convex Nonparametric Least Squares (CNLS) and we found that CNLS is minimum bias estimator in the class of SCKLS estimator. This is on-going research with Daisuke Yagi. This is the first chapter of his dissertation.
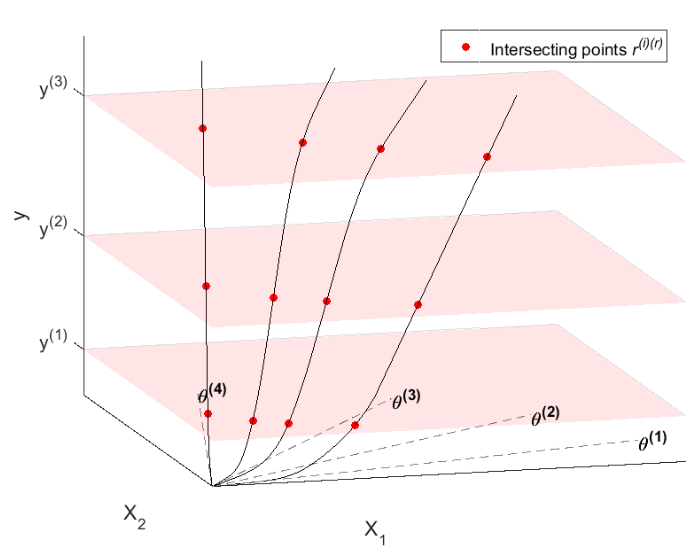
Shape constrained Semi-nonparametric Stochastic Frontiers estimation using a local maximum likelihood approach
We propose a shape-constrained production function estimator starting from the method described in Kumbhakar, Park, Simar, Tsionas 2006 (KPST).
We maximize the loglikelihood of a local linear estimator at each observation. We estimate the parameters for the noise and inefficiency distributions that are potentially heteroscedasticity.
The challenge to imposing shape constraints, such as monotonicity and concavity, is we need to jointly esitmate the maximum likelihood function for all observations while imposing the constraints. This is on-going research with Kevin Layer.
Multi-variate Bayesian Convex Regression with Inefficiency
This research builds on Nonparametric Multi-variate Bayesian Convex Regression to develop a method to estimate shape constrained production frontiers with heteroskedastic inefficiency distributions that scales up to thousands of observations.
We propose a Bayesian method which allows the estimation of a semiparametric production frontiers with a flexible inefficiency distribution, to use panel data and to measure the impact of environmental variables. A Metropolis-Hastings framework is considered to compute smoothed and non-smooth estimates of the production frontier.
Working Paper available at Arxiv.