The estimation of the power curve provides an application for methods to estimate production functions consistent with the regular ultra passum law.

It is well known based on fluid dynamics and kinetic energy that the power generated by a wind turbine follows power curve that appears to be S-shaped. In production economics we also believe the production function has a similar S-shaped when the regular ultra-passim law proposed by Ranger Frisch is satisfied. In this research project executed with Hoon Hwangbo and Yu Ding, we are developing a method to estimate a production function that satisfies the regular ultra passum law, is homothetic, has a single output, and allows for noise in the model. Our goal is to improve estimation in small samples through imposing the shape constraints and to develop methods competitive with kernel regression based methods that are currently widely used in the power curve estimation literature.

Working Paper available at SSRN.

The selection of the direction in the directional distance function provides a way to address some endogeneity issues in the estimation of production functions.

In the summer of 2013, Timo Kuosmanen, Christopher Parmeter, and I taught a week long Ph.D. course before the EWEPA conference at Aalto University. Out of this activity we have had a variety of discussion on various research topics. One of which is the issue of endogeneity in production function models. Olley and Pakes (1996) is widely accepted as the way to estimate production functions in main stream economics. In this paper we propose an alternative that does not require proxies or instruments, but rather uses the flexibility to select the direction in the directional distance function to reduce the endogeneity problems.

Abstract:
The classic econometric approach treats productivity as a residual term of the standard microeconomic production model. Critics of this approach argue that productivity shocks correlate with the input factors that are used as explanatory variables of the regression model, causing simultaneity bias. This paper uses production theory and the known properties of the stochastic distance and directional distance functions to address the simultaneity bias. We first examine the standard cost minimization problem subject to a production function with a multiplicative error term to demonstrate that even if the observed inputs and outputs are endogenous, consistent estimation of the input distance function is possible under certain conditions. This result reveals that the orthogonality conditions required for econometric identification critically depend on the specification of the distance metric, which suggests the directional distance function as one possible solution to the simultaneity problem. We then introduce a general stochastic data generating process of joint production where all inputs and outputs correlate with inefficiency and noise. We show that an appropriately specified direction vector provides the orthogonality conditions required for identification of the directional distance functions. A consistent nonparametric estimator of the directional distance function is developed, which satisfies the essential axioms of the production theory. We examine the specification of the direction vector for the two different purposes of econometric estimation versus efficiency evaluation in an application to electricity distribution firms.

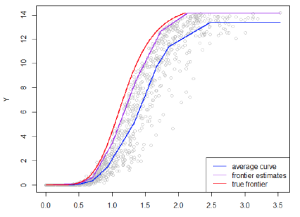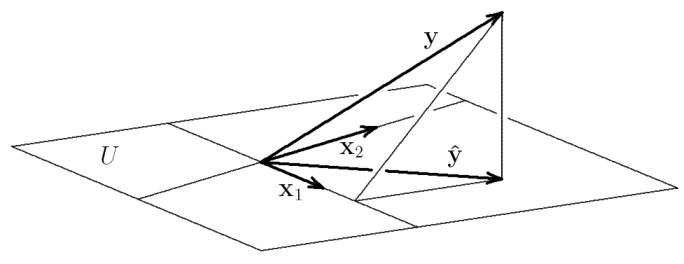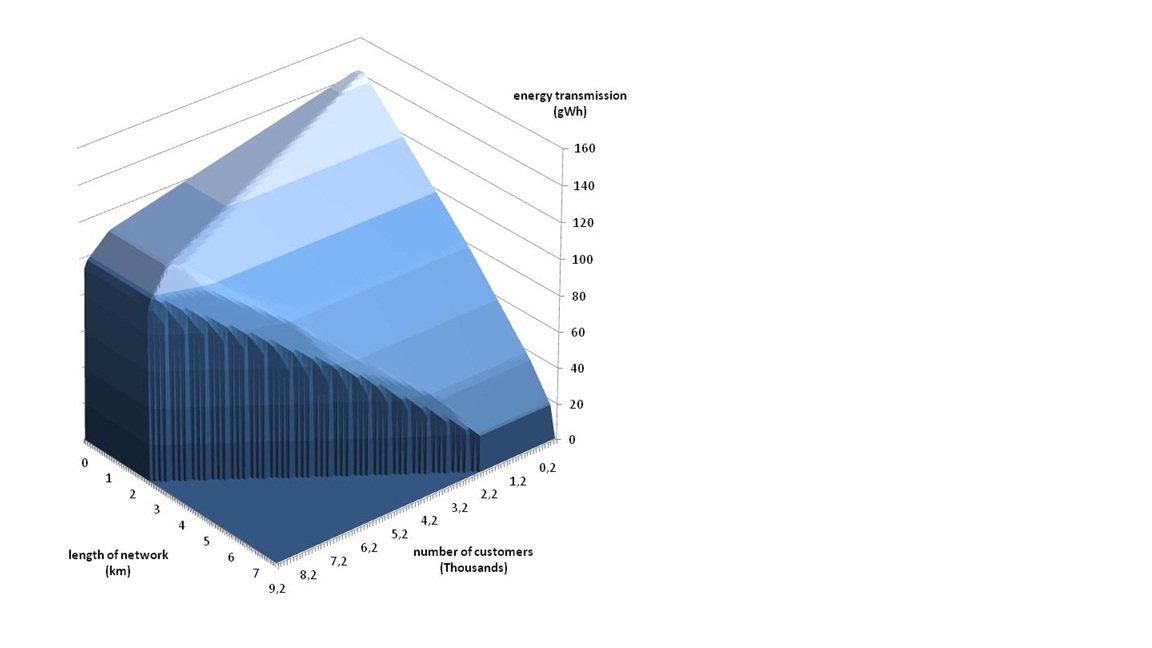
StoNED is the unifying framework for efficiency analysis in which Data Envelopment Analysis and Stochastic Frontier Analysis are specific special cases.

The literature of productive efficiency analysis is divided into two main branches: the parametric Stochastic Frontier Analysis (SFA) and nonparametric Data Envelopment Analysis (DEA). Stochastic Nonparametric Envelopment of Data (StoNED) is a new frontier estimation framework that combines the virtues of both DEA and SFA in a unified approach to frontier analysis. StoNED follows the SFA approach in that it includes a stochastic component decomposed into random noise and inefficiency components imposing the standard SFA assumptions. In contrast to the SFA, however, StoNED does not make any prior assumptions about the functional form of the production function. In that respect, StoNED follows the nonparametric route of DEA, and only imposes free disposability, convexity, and some returns to scale specification. From the postulated class of production functions, the proposed method identifies the production function that best fits the data. The resulting function will always take a piece-wise linear form analogous to the DEA frontiers.

The main advantage of the StoNED approach to the parametric SFA approach is the independence of the ad hoc parametric assumptions about the functional form of the production function (or cost/distance functions). In contrast to the flexible functional forms, one can impose monotonicity, concavity and homogeneity constraints without sacrificing the flexibility of the regression function. On the other hand, the main advantage of StoNED to the nonparametric DEA approach is the better robustness to outliers, data errors, and other stochastic noise in the data. While in DEA the frontier is spanned by a relatively small number of efficient firms, in our method all observations influence the shape of the frontier. Also many standard tools from parametric regression such as goodness of fit statistics and statistical tests are directly applicable in our approach. In summary, StoNED addresses the main points of critique that are usually presented against SFA and DEA, combining the advantages of them both.

read more