Direction Selection in Stochastic Directional Distance Functions

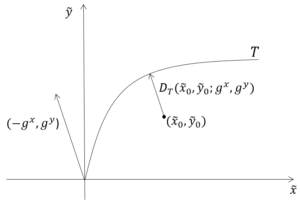
A distance function allows multiple product production using multiple resources to be modeled. A stochastic directional distance function (SDDF) allows for noise in potentially all input and output variables; however when estimated, the direction selected will affect the functional estimates because deviations from the estimated function are minimized in the specified direction. This paper addresses the question, how should the direction be selected to improve the estimates of the underlying production behavior. We are motivated by the estimation of a cost function for hospital production in the U.S., but our insights apply for production and distance functions as well. In contrast to the parameters of the parametric stochastic distance function which are point identified, we show that the parameters of the parametric SDDF are set identified when alternative directions are considered. We present simulation results that show if errors are uncorrelated across variables, then the benefit in terms of improved functional estimates from the use of a directional distance function are significant. Further, we show that these benefits grow as the correlation in error terms across variables grow. This correlation is a type of endogeneity that is common in production settings.
We show that the set of identified parameters for either the parametric or the nonparametric shape constrained estimator can be narrowed via data-driven approaches to restrict the directions considered.
We apply the SDDF estimation procedure to a data set of hospitals containing a sample of approximately 600 hospitals each year from 2005 to 2010. We propose to select a direction that is approximately orthogonal to the estimated function in the central region of the data and find this direction provides significantly better estimates of the cost function relative to other estimators.