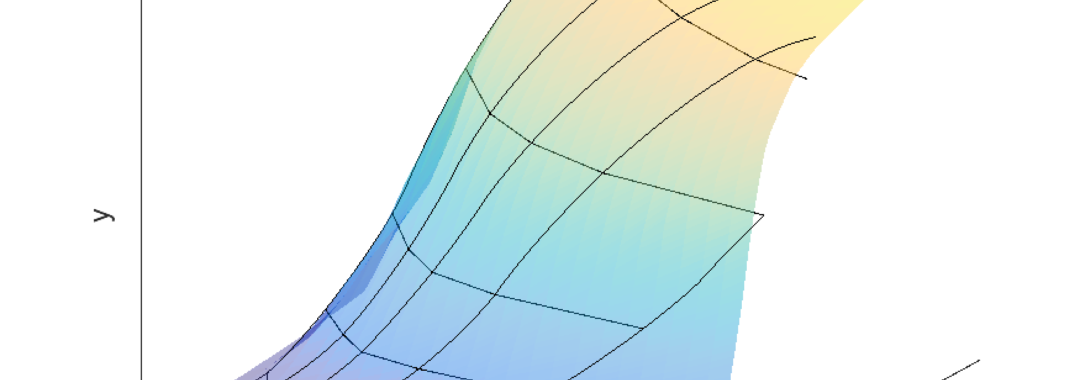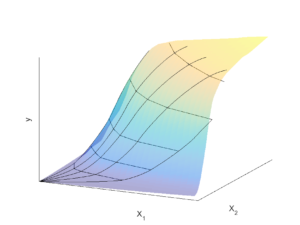
We develop a new approach to estimate a production function based on the economic axioms of the Regular Ultra Passum law and convex non-homothetic input isoquants. Central to the development of our estimator is stating the axioms as shape constraints and using shape constrained nonparametric regression methods.
We implement this approach using data from the Japanese corrugated cardboard industry from 1997-2007. Using this new approach, we find most productive scale size is a function of the capital-to-labor ratio and the largest firms operate close to the largest most productive scale size associated with a high capital-to-labor ratio. We also measure the productivity growth across the panel periods based on the residuals from our axiomatic model. We find that capital-to-labor ratio is negatively correlated with the productivity growth due to the over-investment in capital.
Author Archive: ajohnson
Direction Selection in Stochastic Directional Distance Functions
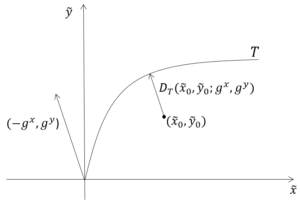
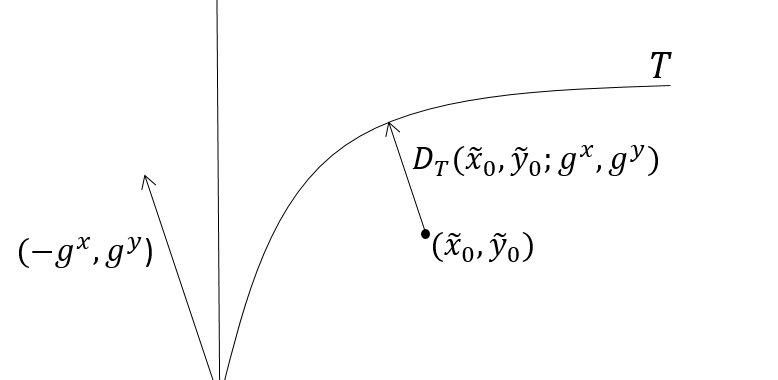
A distance function allows multiple product production using multiple resources to be modeled. A stochastic directional distance function (SDDF) allows for noise in potentially all input and output variables; however when estimated, the direction selected will affect the functional estimates because deviations from the estimated function are minimized in the specified direction. This paper addresses the question, how should the direction be selected to improve the estimates of the underlying production behavior. We are motivated by the estimation of a cost function for hospital production in the U.S., but our insights apply for production and distance functions as well. In contrast to the parameters of the parametric stochastic distance function which are point identified, we show that the parameters of the parametric SDDF are set identified when alternative directions are considered. We present simulation results that show if errors are uncorrelated across variables, then the benefit in terms of improved functional estimates from the use of a directional distance function are significant. Further, we show that these benefits grow as the correlation in error terms across variables grow. This correlation is a type of endogeneity that is common in production settings.
We show that the set of identified parameters for either the parametric or the nonparametric shape constrained estimator can be narrowed via data-driven approaches to restrict the directions considered.
We apply the SDDF estimation procedure to a data set of hospitals containing a sample of approximately 600 hospitals each year from 2005 to 2010. We propose to select a direction that is approximately orthogonal to the estimated function in the central region of the data and find this direction provides significantly better estimates of the cost function relative to other estimators.
Shape Constrained Nonparametric IV Estimators for Production Function Estimation

We propose a shape constrained nonparametric IV estimator which imposes a set of shape constraints on a nonparametric IV approach. We apply the Landweber–Fridman regularization to the Shape Constrained Kernel–weighted Least Squares (SCKLS) estimator developed by Yagi et al. (2018). Furthermore, we also consider more complicated shape constraints proposed by microeconomic theory by applying iterative S–shape algorithm proposed by Yagi et al. (2018). We aim to improve the finite sample performance and the economic interpretability of estimated results by imposing correctly specified shape constraints while avoiding the bias from endogeneity issues.
October 22-25 – Informs Annual Conference – DEA Track – Shape Constrained Estimation of Production Functions
Nonparametric estimation methods avoid functional form misspecification. However, the flexibility of nonparametric methods often cause difficulties in interpreting production function estimates. However, microeconomic theory provides additional structure for modeling a production or cost function which can be interpreted as shape constraints. Several nonparametric shape constrained estimators have been proposed that combine the advantage of avoiding functional misspecification with improving the interpretability of estimation results. We will review the recent work by our research team in this area.
Jan 28-Feb 2, 2018 – Shape-Constrained Methods: Inference, Applications, and Practice – Banff International Research Station, Alberta, Canada
Estimation in shape-constrained statistical models dates back at least as far as Hildreth [(1954); J. Amer. Statist. Assoc., 49, 598–619], who considered the maximum likelihood estimation of production functions under the natural assumption of non-increasing returns (which implies that the production function is concave and nondecreasing). Around the same time, Grenander [(1956); Skand. Aktuarietidskr., 39, 125–153], motivated by the theory of mortality measurement, studied the nonparametric maximum likelihood estimator of a decreasing density function on the positive half line. Over subsequent years, these ideas have been extended and developed in many different directions.
Shape-constrained methods may be applied to regression function estimation as well as density estimation, and allow the user to implement vague and qualitative assumptions about functional forms, without having to specify parametric models. This is extremely useful in the common situation where the only valid assumptions involve shape (and smoothness). Being nonparametric, the methods are more robust than standard parametric approaches. Further, although these methods deal with infinite- dimensional models (e.g., functions), estimation can still be carried out using the method of maximum likelihood (probably the main technique for estimation of parameters in a statistical model).
June 19 – Lancaster University – Regulating Local Monopolies in Electricity Distribution: An Application of Shape Constrained Regression
The Finnish electricity market has a competitive energy generation market and a monopolistic distribution system. To regulate the local monopoly power of network operators, the government regulator uses frontier estimation methods to identify excessive distribution costs, taking into account outputs and the operating environment. We describe the new regulatory system developed for the Finnish regulator, which is based on shape constrained nonparametric functional estimation and utilizes panel data to detect the excessive costs from random noise.
The literature of productive efficiency analysis is divided into two main branches: the parametric SFA and nonparametric DEA. A new method is proposed, Stochastic Nonparametric Envelopment of Data, StoNED, that combines the virtues of both DEA and SFA in a unified approach to frontier analysis. StoNED follows the SFA approach by including a stochastic component. In contrast to SFA, however, the proposed method does not make any prior assumptions about the functional form of the production function. In that respect, StoNED is similar to DEA, and only imposes free disposability, convexity, and some returns to scale specification.
The main advantage of the StoNED approach to the parametric SFA approach is the independence of the ad hoc parametric assumptions about the functional form of the production function (or cost/distance functions). In contrast to the flexible functional forms, one can impose monotonicity, concavity and homogeneity constraints without sacrificing the flexibility of the regression function. Additionally, the main advantage of StoNED to the nonparametric DEA approach is robustness to outliers, data errors, and other stochastic noise in the data. In DEA the frontier is spanned by a relatively small number of efficient firms, however, in our method all observations influence the shape and level of the frontier. Also many standard tools from parametric regression such as goodness of fit statistics and statistical tests are directly applicable in our approach. This is collaborate work with Timo Kuosmanen of Aalto University in Finland.
March 6 – Department of Industrial and Systems Engineering, Virginia Tech – Regulating Local Monopolies in Electricity Distribution: An Application of Shape Constrained Regression
The Finnish electricity market has a competitive energy generation market and a monopolistic distribution system. To regulate the local monopoly power of network operators, the government regulator uses frontier estimation methods to identify excessive distribution costs, taking into account outputs and the operating environment. We describe the new regulatory system developed for the Finnish regulator, which is based on shape constrained nonparametric functional estimation and utilizes panel data to detect the excessive costs from random noise.
The literature of productive efficiency analysis is divided into two main branches: the parametric SFA and nonparametric DEA. A new method is proposed, Stochastic Nonparametric Envelopment of Data, StoNED, that combines the virtues of both DEA and SFA in a unified approach to frontier analysis. StoNED follows the SFA approach by including a stochastic component. In contrast to SFA, however, the proposed method does not make any prior assumptions about the functional form of the production function. In that respect, StoNED is similar to DEA, and only imposes free disposability, convexity, and some returns to scale specification.
The main advantage of the StoNED approach to the parametric SFA approach is the independence of the ad hoc parametric assumptions about the functional form of the production function (or cost/distance functions). In contrast to the flexible functional forms, one can impose monotonicity, concavity and homogeneity constraints without sacrificing the flexibility of the regression function. Additionally, the main advantage of StoNED to the nonparametric DEA approach is robustness to outliers, data errors, and other stochastic noise in the data. In DEA the frontier is spanned by a relatively small number of efficient firms, however, in our method all observations influence the shape and level of the frontier. Also many standard tools from parametric regression such as goodness of fit statistics and statistical tests are directly applicable in our approach. This is collaborate work with Timo Kuosmanen of Aalto University in Finland.
February 1 – Department of Economics, Rice University – Regulating Local Monopolies in Electricity Distribution: An Application of Shape Constrained Regression
The Finnish electricity market has a competitive energy generation market and a monopolistic distribution system. To regulate the local monopoly power of network operators, the government regulator uses frontier estimation methods to identify excessive distribution costs, taking into account outputs and the operating environment. We describe the new regulatory system developed for the Finnish regulator, which is based on shape constrained nonparametric functional estimation and utilizes panel data to detect the excessive costs from random noise.
The literature of productive efficiency analysis is divided into two main branches: the parametric SFA and nonparametric DEA. A new method is proposed, Stochastic Nonparametric Envelopment of Data, StoNED, that combines the virtues of both DEA and SFA in a unified approach to frontier analysis. StoNED follows the SFA approach by including a stochastic component. In contrast to SFA, however, the proposed method does not make any prior assumptions about the functional form of the production function. In that respect, StoNED is similar to DEA, and only imposes free disposability, convexity, and some returns to scale specification.
The main advantage of the StoNED approach to the parametric SFA approach is the independence of the ad hoc parametric assumptions about the functional form of the production function (or cost/distance functions). In contrast to the flexible functional forms, one can impose monotonicity, concavity and homogeneity constraints without sacrificing the flexibility of the regression function. Additionally, the main advantage of StoNED to the nonparametric DEA approach is robustness to outliers, data errors, and other stochastic noise in the data. In DEA the frontier is spanned by a relatively small number of efficient firms, however, in our method all observations influence the shape and level of the frontier. Also many standard tools from parametric regression such as goodness of fit statistics and statistical tests are directly applicable in our approach. This is collaborate work with Timo Kuosmanen of Aalto University in Finland.
July 31 – August 1 – NBER Japan Project Meeting 2017 – Tokyo, Japan

The annual general research conference on the Japanese economy will be held July 31, 2017 in Tokyo. The conference will be jointly sponsored by the NBER, Australia-Japan Research Centre, Center for Advanced Research in Finance, and the Center for Japanese Economy and Business. Last years conference was highlighted by papers by Robert Delke and Hajime Tomura with outstanding discussants such as Nobuhiro Kiyotaki and Stephen Redding.
Economic and Social Research Institute (ESRI) will hold their annual research conference on August 1st, 2017 following the NBER Japan project meeting.
The Economic and Social Research Institute (ESRI) was founded in January 2001 as part of the Cabinet Office with the expansion of the functions and scale of the Economic Planning Agency’s Economic Research Institute under the reorganization of Japan’s central government ministries and agencies. Known as the “forum for knowledge” for the Cabinet, the Cabinet Office is in charge of key administrative issues. As the Cabinet Office’s think tank, the ESRI could rightly be called the “forum for knowledge” within the “forum for knowledge” because the ESRI links theory with policy.
The main role of the ESRI is to strengthen its functions as a policy research institute by conducting theoretical and experimental research related to economic activities and policies, social activities, and other issues. The ESRI also trains and develops human resources to spearhead policy research. In addition, the ESRI compiles and publishes estimates for the gross domestic product (GDP) and other statistics in the System of National Accounts (SNA). The ESRI publishes both the Preliminary Quarterly GDP Estimates and the Annual Report on National Accounts. Moreover, the ESRI compiles and publishes the Coincident Index and other business statistics.