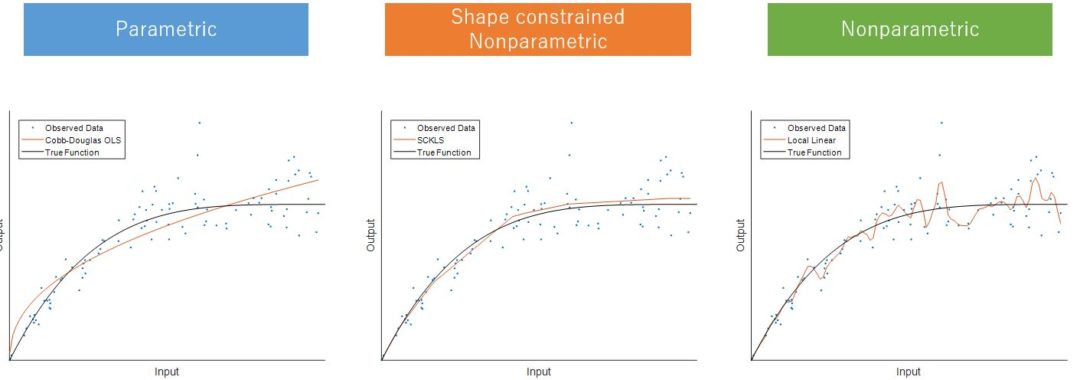
Census of manufacturing data is gathered by statistical agency around the world and can be used to benchmark performance within industries or summarize production behavior within industries. In this talk, I present results our laboratory have found for data from the U.S., Japan and Chile. I present some of the modeling challenges and limitations of the data. I focus on the use of nonparametric shape constrained production function estimators and describe some of the benefits that result from their use. I close with a variety of policy insights that can be gained from analyzing Census of manufacturing data.

Category Archives: Seminars
December 14 – Operations Research Society of Japan – Kansai Chapter – Computational Complexity of Shape Constrained Estimation
Production function estimation using nonparametric shape constrained methods can be computationally challenging. For the standard additive error model, y = f(x) + ε, with monotonicity and concavity constraints imposed at each observation, the associated programming problem has a quadratic objective function and linear inequality constraints and thus is easy from a computational complexity point of view. However, the number of constraints grows at the rate n2. Thus, estimation on a grid, as described in Preciado Arreola et al. (2016) and Yagi et al. (2018), can reduce the computational difficulty significantly. In contrast, the multiplicative error model, y = f(x) eε, which models heteroskedasticity in the error term with monotonicity and concavity constraints has a quasi-convex objective function requiring generally non-linear optimization methods. We discuss these and other computational issues related to nonparametric shape constrained methods.
September 6 – Penn State – Shaped constrained estimation and some applications
Assumptions motivated by either logical or existing theory can be imposed during model estimation to restrict the feasible region of the parameters. The restrictions, implemented as shape constraints, may not provide any benefits in an asymptotic analysis, but will improve the estimator’s finite sample performance. This paper briefly reviews an illustrative set of research on shape constrained estimation in the economics and operations research literature. We highlight the methodological innovations and applications, with a particular emphasis on utility functions, production economics, and sequential decision making applications.
June 12-15 – North American Productivity Workshop – Axiomatic Nonparametric Production Functions: Relaxing Concavity and Homotheticity
We develop a new approach to estimate a production function based on the economic axioms of the Regular Ultra Passum law and convex non-homothetic input isoquants. Central to the development of our estimator is stating the axioms as shape constraints and using shape constrained nonparametric regression methods.
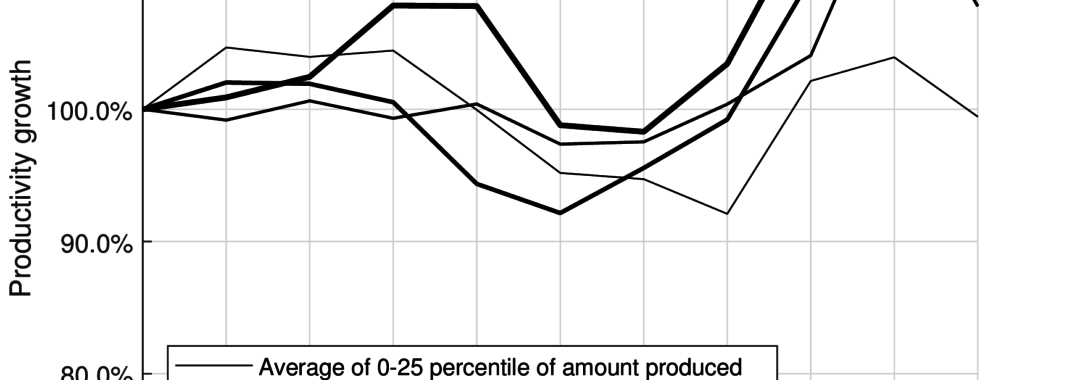
We implement this approach using data from the Japanese corrugated cardboard industry from 1997-2007. Using this new approach, we find most productive scale size is a function of the capital-to-labor ratio and the largest firms operate close to the largest most productive scale size associated with a high capital-to-labor ratio. We also measure the productivity growth across the panel periods based on the residuals from our axiomatic model. We find that capital-to-labor ratio is negatively correlated with the productivity growth due to the over-investment in capital.
May 17 – Center for Operations Research and Econometrics: UC Louvain – Shape constrained kernel-weighted least squares: Application to production function estimation for Chilean manufacturing industries
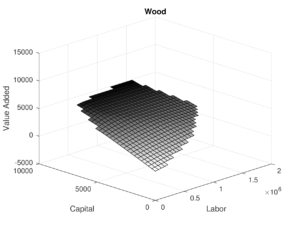
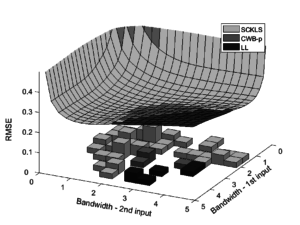
We examine a novel way of imposing shape constraints on a local polynomial kernel estimator. The proposed approach is referred to as Shape Constrained Kernel-weighted Least Squares (SCKLS). We prove uniform consistency of the SCKLS estimator with monotonicity and convexity/concavity constraints and establish its convergence rate.
In addition, we propose a test to validate whether shape constraints are correctly specified.
The competitiveness of SCKLS is shown in a comprehensive simulation study. Finally, we analyze Chilean manufacturing data using the SCKLS estimator and quantify production in the plastics and wood industries. The results show that exporting firms have significantly higher productivity.
May 14 – KU Leuven – Shape constrained kernel-weighted least squares: Application to production function estimation for Chilean manufacturing industries
We examine a novel way of imposing shape constraints on a local polynomial kernel estimator. The proposed approach is referred to as Shape Constrained Kernel-weighted Least Squares (SCKLS). We prove uniform consistency of the SCKLS estimator with monotonicity and convexity/concavity constraints and establish its convergence rate.
In addition, we propose a test to validate whether shape constraints are correctly specified.
The competitiveness of SCKLS is shown in a comprehensive simulation study. Finally, we analyze Chilean manufacturing data using the SCKLS estimator and quantify production in the plastics and wood industries. The results show that exporting firms have significantly higher productivity.
May 4-7 – POMS – Shape constrained kernel-weighted least squares: Application to production function estimation for Chilean manufacturing industries

We examine a novel way of imposing shape constraints on a local polynomial kernel estimator. The proposed approach is referred to as Shape Constrained Kernel-weighted Least Squares (SCKLS). We prove uniform consistency of the SCKLS estimator with monotonicity and convexity/concavity constraints and establish its convergence rate.
In addition, we propose a test to validate whether shape constraints are correctly specified.
The competitiveness of SCKLS is shown in a comprehensive simulation study. Finally, we analyze Chilean manufacturing data using the SCKLS estimator and quantify production in the plastics and wood industries. The results show that exporting firms have significantly higher productivity.
Jan 28-Feb 2, 2018 – Shape-Constrained Methods: Inference, Applications, and Practice – Nonparametric S-shape Estimation: Modeling firm expansion and consolidation in the Japanese Cardboard Industry

We develop a new approach to estimate a production function based on the economic axioms of the Regular Ultra Passum law and convex non-homothetic input isoquants. Central to the development of our estimator is stating the axioms as shape constraints and using shape constrained nonparametric regression methods.
We implement this approach using data from the Japanese corrugated cardboard industry from 1997-2007. Using this new approach, we find most productive scale size is a function of the capital-to-labor ratio and the largest firms operate close to the largest most productive scale size associated with a high capital-to-labor ratio. We also measure the productivity growth across the panel periods based on the residuals from our axiomatic model. We find that capital-to-labor ratio is negatively correlated with the productivity growth due to the over-investment in capital.
October 22-25 – Informs Annual Conference – DEA Track – Shape Constrained Estimation of Production Functions
Nonparametric estimation methods avoid functional form misspecification. However, the flexibility of nonparametric methods often cause difficulties in interpreting production function estimates. However, microeconomic theory provides additional structure for modeling a production or cost function which can be interpreted as shape constraints. Several nonparametric shape constrained estimators have been proposed that combine the advantage of avoiding functional misspecification with improving the interpretability of estimation results. We will review the recent work by our research team in this area.
June 19 – Lancaster University – Regulating Local Monopolies in Electricity Distribution: An Application of Shape Constrained Regression
The Finnish electricity market has a competitive energy generation market and a monopolistic distribution system. To regulate the local monopoly power of network operators, the government regulator uses frontier estimation methods to identify excessive distribution costs, taking into account outputs and the operating environment. We describe the new regulatory system developed for the Finnish regulator, which is based on shape constrained nonparametric functional estimation and utilizes panel data to detect the excessive costs from random noise.
The literature of productive efficiency analysis is divided into two main branches: the parametric SFA and nonparametric DEA. A new method is proposed, Stochastic Nonparametric Envelopment of Data, StoNED, that combines the virtues of both DEA and SFA in a unified approach to frontier analysis. StoNED follows the SFA approach by including a stochastic component. In contrast to SFA, however, the proposed method does not make any prior assumptions about the functional form of the production function. In that respect, StoNED is similar to DEA, and only imposes free disposability, convexity, and some returns to scale specification.
The main advantage of the StoNED approach to the parametric SFA approach is the independence of the ad hoc parametric assumptions about the functional form of the production function (or cost/distance functions). In contrast to the flexible functional forms, one can impose monotonicity, concavity and homogeneity constraints without sacrificing the flexibility of the regression function. Additionally, the main advantage of StoNED to the nonparametric DEA approach is robustness to outliers, data errors, and other stochastic noise in the data. In DEA the frontier is spanned by a relatively small number of efficient firms, however, in our method all observations influence the shape and level of the frontier. Also many standard tools from parametric regression such as goodness of fit statistics and statistical tests are directly applicable in our approach. This is collaborate work with Timo Kuosmanen of Aalto University in Finland.